Resumo média simples, ponderada, mediana, moda

A Média Aritmética de um conjunto de dados é obtida somando todos os valores e dividindo o valor encontrado pelo número de dados desse conjunto.

É muito utilizada em estatística como uma medida de tendência central.

Pode ser simples, onde todos os valores possuem a mesma importância, ou ponderada, quando considera pesos diferentes aos dados.

Média Aritmética Simples

Esse tipo de média funciona de forma mais adequada quando os valores são relativamente uniformes.

Por ser sensível aos dados, nem sempre fornece os resultados mais adequados.

Isso porque todos os dados possuem a mesma importância (peso).

Fórmula

Onde,

M_s: média aritmética simples
x₁, x₂, x₃,...,x_n: valores dos dados
n: número de dados

Exemplo:

Sabendo que as notas de um aluno foram: 8,2; 7,8; 10,0; 9,5; 6,7, qual a média que ele obteve no curso?

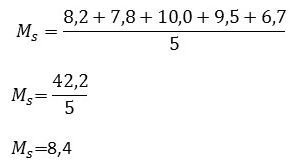
Média Aritmética Ponderada

A média aritmética ponderada é calculada multiplicando cada valor do conjunto de dados pelo seu peso.

Depois, encontra-se a soma desses valores que será dividida pela soma dos pesos.

Fórmula

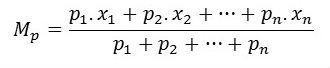
Onde,

M_p: Média aritmética ponderada
p₁, p₂,..., p_n: pesos
x₁, x₂,...,x_n: valores dos dados

Exemplo:

Considerando as notas e os respectivos pesos de cada uma delas, indique qual a média que o aluno obteve no curso.

Disciplina	Nota	Peso
Biologia	8,2	3
Filosofia	10,0	2
Física	9,5	4
Geografia	7,8	2
História	10,0	2
Língua Portuguesa	9,5	3
Matemática	6,7	4

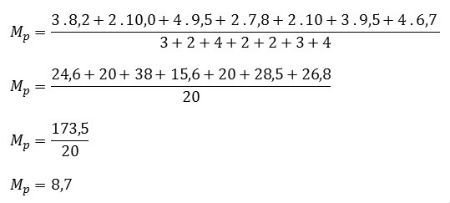
Moda

Moda (M_o) é o valor mais frequente num conjunto de dados.

Como Calcular?

Não há fórmula para calcular a moda. Para tanto, basta observar a frequência com que os valores aparecem.

Exemplo:

{32, 27, 15, 44, 15}
M_o = 15

É chamada bimodal quando há mais do que uma medida com maior frequência:

{32, 27, 15, 44, 15, 32}
M_o = 32 ou 15

Mediana

Mediana (M_d) é o valor que medeia os valores presentes num conjunto ordenado numericamente.

Como Calcular?

Primeiro é preciso colocar os valores em ordem crescente ou decrescente para, de seguida, encontrar o centro do conjunto.

Exemplo:

{32, 27, 15, 44, 15}

{15, 15, 27, 32, 44}
M_d = 27

Quando o número de valores presentes no conjunto é par, a mediana é encontrada pela média dos dois valores centrais. Assim, esses valores são somados e divididos por dois, ou seja, n + n / 2.

Exemplo:

{32, 27, 15, 44, 15, 32}

{15, 15, 27, 32, 32, 44}
M_d = 27 + 32 / 2
M_d = 59 / 2
M_d = 29,5